1. Qué es un vector?
2. Cuándo dos vectores son iguales?
3. Cómo se determina el ángulo entre dos vectores?
4. Qué es la dirección de un vector?
5. Qué es el sentido de un vector?
6. Qué es un escalar?
7. Qué es un paralelogramo?
8. En qué consiste la suma de vectores por el método del triángulo?
9. En qué consiste la suma de vectores por el método del paralelogramo?
10. Qué son vectores unitarios?
11. qué es y cómo se define por el modelo matemático el producto escalar de vectores?
12. Cuál es el modelo matemático para determinar el ángulo entre dos vectores?
13. Qué es momento de una fuerza?
14. En forma escalar cual es el modelo matemático para determinar el momento de una fuerza F respecto de un punto P?
15. En el sistema de unidades F.P.S. cuales son las unidades para el momento de una fuerza?
16. En el Sistema Internacional de Unidades cuales son las unidades para el momento de una fuerza?
17. Cuando una fuerza actúa en la misma dirección del vector de posición, esta fuerza produce tendencia de giro?
18. Que es el Principio de Transmisibilidad de una Fuerza?
19. Que maneras existen para multiplicar dos vectores?
20. Si el modelo matemático indica que el momento de una fuerza es de signo negativo, la norma general como interpreta ese signo?
1. Hallar la fuerza resultante FR del sistema mostrado aplicando el método del paralelogramo y el método analítico.
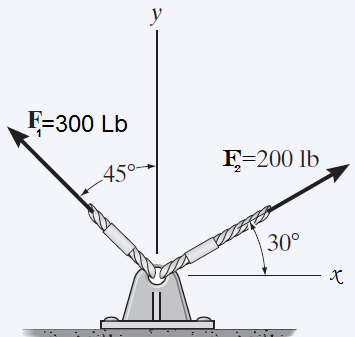
2. Hallar la fuerza resultante FR del sistema mostrado aplicando el método del paralelogramo y el método analítico.
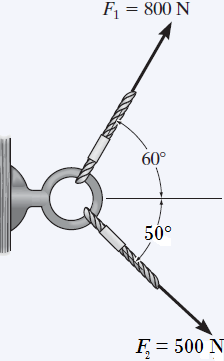
3. Hallar la fuerza resultante FR del sistema mostrado aplicando el método del paralelogramo y el método analítico.
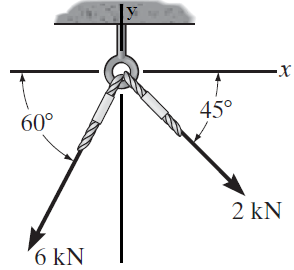
4. Hallar la fuerza resultante FR del sistema mostrado aplicando el método del paralelogramo y el método analítico.
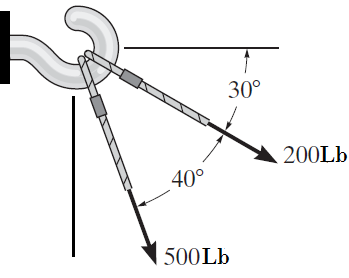
5. Hallar la fuerza resultante FR del sistema mostrado aplicando el método del paralelogramo y el método analítico.
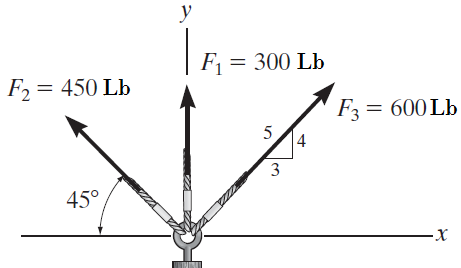
6. Determine la magnitud de la fuerza F3 y su dirección θ para que la fuerza resultante FR del sistema mostrado sea: FR=99.76 N28.37↗
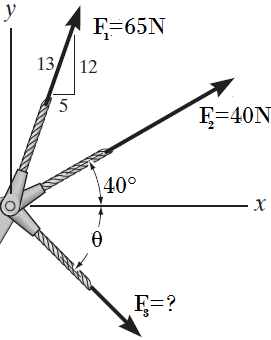
7. Cuál es la dirección θ y magnitud de una fuerza F1 que haga posible que fuerza resultante del sistema sea como se muestra.
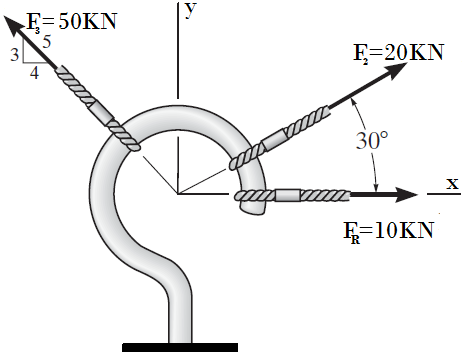
8. Hallar la fuerza resultante FR del sistema mostrado aplicando el método del paralelogramo y el método analítico.
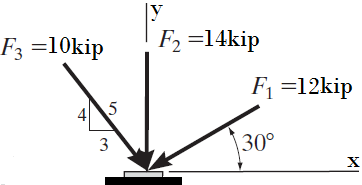
9. Determine la magnitud de la fuerza F3 y su dirección θ para que la fuerza resultante FR del sistema mostrado sea: FR=80 Lb15↘
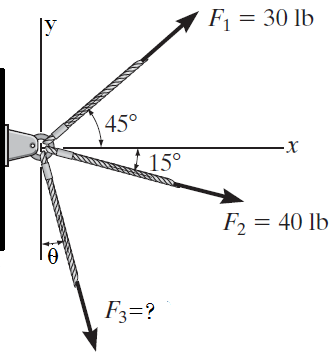
10. Determine la magnitud de la fuerza F1 y su dirección θ para que la fuerza resultante FR del sistema mostrado sea igual a 0
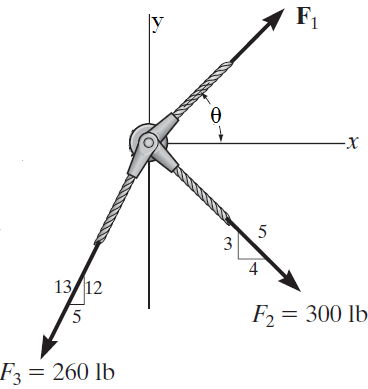
11. Hallar el momento de la fuerza F respecto del punto A haciendo uso del método escalar y del método vectorial.
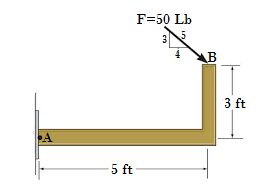
12. Hallar el momento resultante de las fuerzas F1 y F2 respecto del punto P haciendo uso del método escalar y del método vectorial.
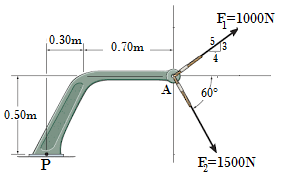
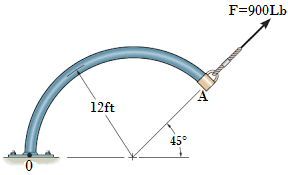
13. Hallar el momento de la fuerza F respecto del punto P haciendo uso del método escalar y del método vectorial.
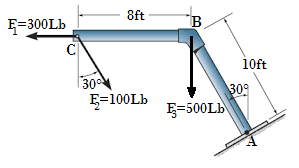
14. Hallar el momento resultante de las fuerzas F1, F2 y F3 respecto del punto P haciendo uso del método escalar y del método vectorial.
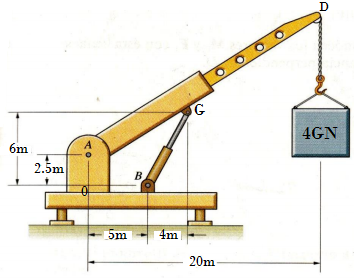
15. Cuál es la magnitud y dirección de la fuerza FC que hace el cilindro hidráulico sobre el brazo de la grua para que la grua permanesca en equilibrio. El brazo de la grua tiene un peso de 6 GN y se concentra en el punto G
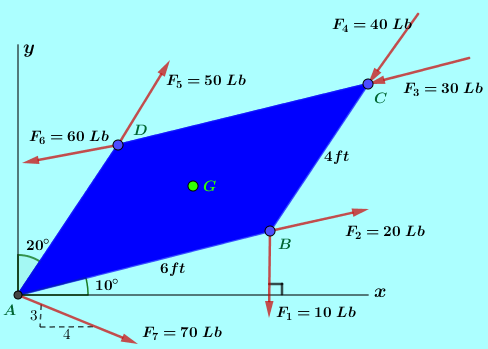
16. Determinar el momento resultante del sistema de fuerzas que actúan sobre la placa de 2.5slug. El peso de la placa se considera concentrado en el centro de la placa (en el punto G).
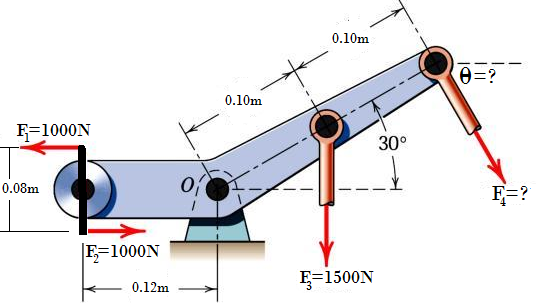
17. Cuál es el mínimo valor de la fuerza F4 y su dirección θ correspondiente, para que el momento resultante respecto del punto 0 sea igual a cero.
18. Determine el ángulo θ entre el vector F1=[3i+6j−9k]N y el vector F2=[−2i+4j+4k]N
19. Determine el ángulo θ entre el vector F=[−8i−4j+2k]Lb y el vector r=[−2i+10j+10k]ft
20. Determine el ángulo θ entre el vector r1=[5i+5j+5k]m y el vector F2=[−5i−5j−5k]m